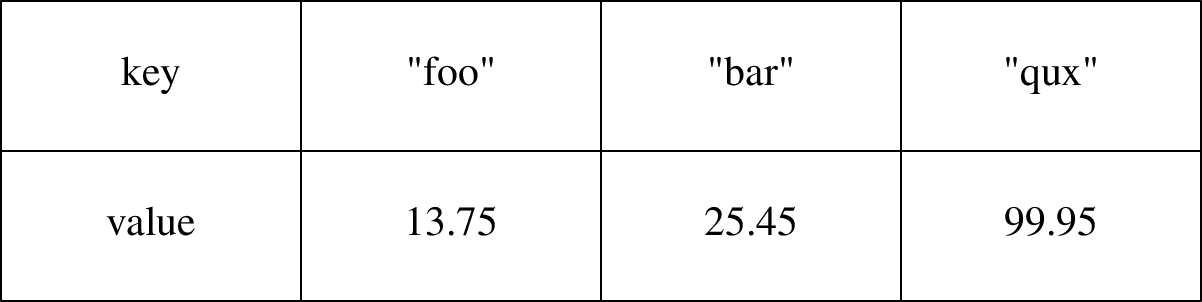Teilweise Strukturierte Daten
Der Begriff der teilweise strukturierten, halbstrukturierten oder semistrukturierten Daten ist weniger genau definiert als derjenige der strukturierten Daten. Manche Definitionen des Begriffs verwenden das Vorhandensein von Metadaten (Zusatzdaten) als Kriterium: Demnach sind teilweise strukturierte Daten unstrukturierte Daten, die um Meta-Daten angereichert worden sind. Anhand dieser Metadaten (z.B. Erstellungsdatum, Autor usw.) lassen sich die sonst unstrukturierten Daten (z.B. Dokumente) einordnen.
In anderen Definitionen werden teilweise strukturierte Daten als Datenformate angesehen, deren Form zwar vorgegeben ist (z.B. JSON, XML, CSV), die konkreten Inhalte jedoch nicht einem bestimmten Schema folgen müssen.
Im Block zu strukturierten Daten haben wir gesehen, dass sich Objekte aus der realen Welt im Programmcode mittels Klassen bzw. Strukturen, in relationalen Datenbanken mittels Relationen bzw. Tabellen und in NoSQL-Datenbanken beispielsweise als Dokumente abbilden lassen.
In der Informatik bildet man nicht nur Objekte aus der realen Welt wie z.B. Personen oder Adressen ab, sondern oftmals auch nur Teilaspekte von diesen Objekten, z.B. eine Liste bekannter Vornamen oder eine Zuordnung von Postleitzahlen zu Orten. Solche Sachverhalte bildet man im Programmcode durch sogenannte abstrakte Datentypen ab, die persistent in verschiedenen Arten von Services verwaltet werden können (z.B. in einem Key-Value-Store, in einer Message Queue oder in einer Time-Series-Datenbank).
Diese abstrakten Datentypen müssen für einen konkreten Einsatzzweck genauer spezifiziert werden. Verwendet man eine Liste, muss man sich bewusst sein, welchen Datentyp die einzelnen Listenelemente haben. Verwendet man eine Map, muss man für die Schlüssel und die Werte einen Datentyp definieren.
Im Rahmen dieses Moduls sollen teilweise strukturierte Daten als abstrakte Datentypen betrachtet werden, die sich über einen Service verwalten und bei Bedarf persistent abspeichern lassen. Im Gegensatz zu strukturierten Daten kann dieser Service jedoch nur gewisse Eigenschaften dieser Daten garantieren (z.B. ob es sich um eine Liste mit mehrdeutigen oder um eine Menge mit eindeutigen Elementen handelt), aber kein Schema für diese Daten forcieren (z.B. dass ein Listeneintrag über einen Vor- und Nachnamen verfügen muss).
Abstrakte Datentypen
Im Gegensatz zu einem konkreten Datentyp wie einer class Person oder struct Address sind abstrakte Datentypen weniger spezifisch auf ein bestimmtes Einsatzgebiet eingeschränkt. Man kann sie sehr flexibel für die verschiedensten Probleme verwenden, wobei es wichtig ist, für das vorliegende Problem die richtige Datenstruktur zu wählen.
Möchte man beispielsweise die Hierarchie eines Dateisystems oder ein Organigramm einer Firma abbilden, eignet sich hierzu ein Baum (engl. Tree) als abstrakter Datentyp. Möchte man hingegen bloss eine Reihe von Messwerten abspeichern, ist ein Array oder eine Liste der geeignete abstrakte Datentyp. Sind die Elemente einer Liste bzw. eines Arrays eindeutig, und ist deren Reihenfolge nicht relevant, kann man diese als eine Menge (engl. Set) abbilden. Möchte man Werte nach einem bestimmten Schlüssel nachschlagen können, sind Maps bzw. Hashes die richtige Wahl.
Arrays
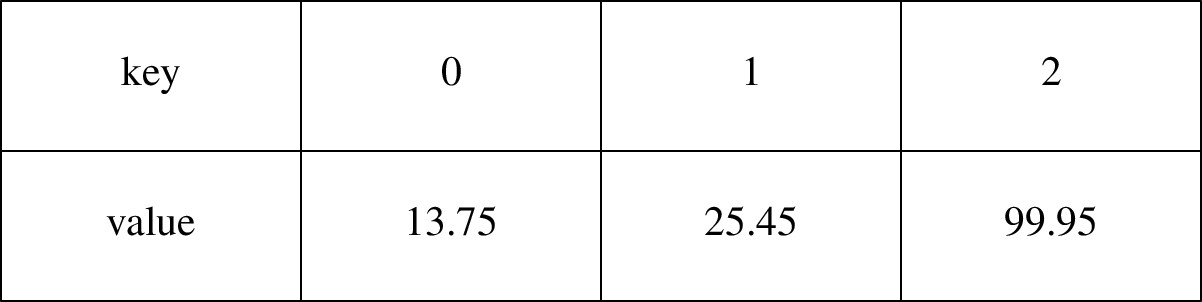
Ein Array ist eine Datenstruktur, welche ihre Elemente unter Indizes von [0..n[ ablegt, d.h. 0 (inklusiv) ist der kleinste Index, n (exklusiv, d.h.n-1) ist der höchste Index.
Listen
Im Gegensatz zu Arrays werden Listen nicht über einen Index geordnet, sondern speichern zu jedem Element eine Referenz auf dessen Nachfolger ab:
Das letzte Element einer Liste verweist auf null um zu signalisieren, dass die
Liste zu Ende ist.
Vergleich Arrays und Listen
Das gleiche Problem kann sowohl mit Arrays als auch mit Listen gelöst werden,
es gibt aber massive Unterschiede in der Performance für verschiedene
Operationen auf den beiden Datenstrukturen. Angenommen, man möchte eine
Datenstruktur mit n Elementen verwalten, ergeben sich dadurch folgende
Unterschiede:
| Operation | Schritte (Array) | Schritte (Liste) |
|---|---|---|
| Zugriff auf bestimmtes Element | 1 | durschnittlich: n/2 |
| vorne anfügen | n | 1 |
| hinten anfügen | 1 oder n+1 | 1 oder n+1 |
- Beim Anfügen an ein Array benötigt man einen Schritt, wenn das Array hinten
noch freie Plätze reserviert hat. Hat das Array keine Kapazität für weitere
Elemente, muss ein grösseres Array erstellt werden, in welches dann alle
Einträge des bestehenden Arrays kopiert werden müssen. Dadurch werden
n+1Schritte benötigt. - Beim Anfügen an eine Liste kommt es darauf an, ob eine Referenz zum letzten
Element gespeichert wird. Ist eine solche Referenz vorhanden, kann ein
weiteres Element in einem Schritt hinzugefügt werden. Andernfalls benötigt man
n+1Schritte, da man zuerst noch innSchritten das Ende der Liste suchen muss.
Mengen (Sets)
Eine Menge bzw. ein Set ist eine ungeordnete Ansammlung von eindeutigen Elementen. Betrachten wir die folgenden beiden Mengen A und B:
- $ A = \{1, 2, 3, 4, 5\} $
- $ B = \{2, 4, 6, 8, 10\} $
Auf diese Mengen können verschiedene Mengenoperationen angewendet werden:
- Schnittmenge: $ A \cap B = \{2, 4\} $
- Vereinigungsmenge: $ A \cup B = \{1, 2, 3, 4, 5, 6, 8, 10 \} $
- Differenz (“A ohne B”): $ A - B = \{1, 3, 5\} $
- Differenz (“B ohne A”): $ B - A = \{6, 8, 10\} $
Maps bzw. Hashes
Eine Map oder ein Hash ist eine Datenstruktur, die arbiträre d.h. beliebige Indizes unterstützt:
Die Indizes müssen auch hier eindeutig sein, aber keinem bestimmten Schema folgen. Die Indizes kann man sich als eine Menge (Set) vorstellen, in welcher alle Elemente eindeutig sein müssen.
Maps haben in verschiedenen Programmiersprachen verschiedene Bezeichnungen: Map (Go), Dictionary (Python), Hash (Ruby), Table (Lua), assoziatives Array (PHP) usw.
Weiterführende Literatur
Die folgenden beiden Bücher bieten weiterführende Informationen zu abstrakten Datentypen bzw. Datenstrukturen und deren Verarbeitung mithilfe verschiedenster Algorithmen:
- Jay Wengrow: A Common-Sense Guide to Data Structures and Algorithms
- Adita Bhargava: Grokking Algorithms